时空是一体（本体）的统一的，函数式、命令式是一体（本体）的统一的。

图1

图2
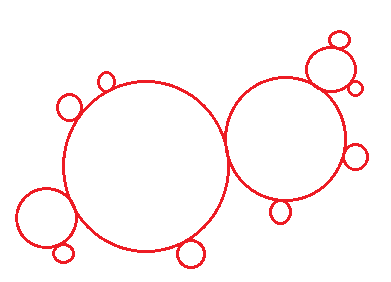
上面两个图是计算机里的对象空间和对象的运动轨迹，这两种有限集合图可能是同一个图。被cpu线程驱动的主体对象沿着红线行走，前一个图是主体观察到的左手边的世界，后一个图是主体观察到的自己右手边的世界。

一致的世界，所有地方都一致，明确无歧义。

图3
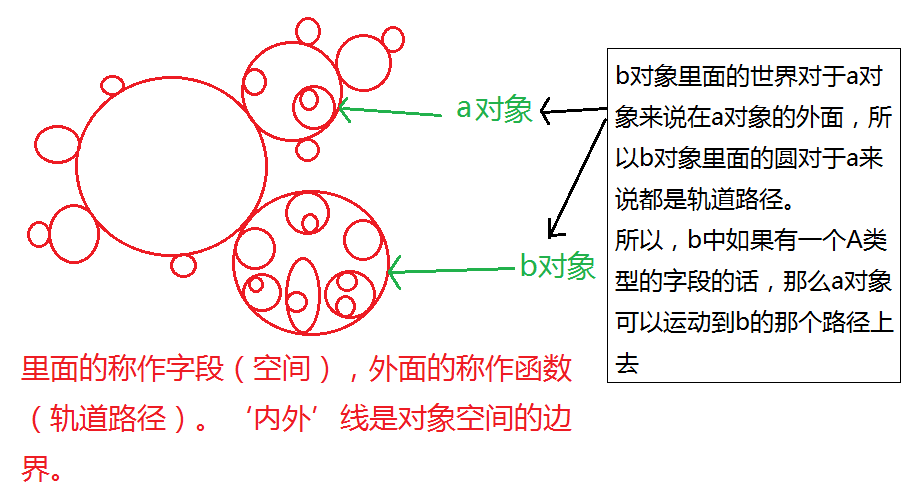
上图有很多圆，圆里面的圆（表集合、空间）称作字段，圆外面的圆称作函数（轨道路径）。“内外”边界（线、曲面）是对象空间的边界线、边界面。上图使用图形明确标出了什么是对象？比如两个绿色箭头指向的那两个圆体就是对象。
b对象里面的世界对于a对象来说在a对象的外面，所以b对象里面的圆对于a来说不是a的字段而是a可能可以途经的轨道路径。所以，b中如果有一个A类型的字段的话，那么a对象就可以运动到b的那个字段位置地去。什么叫A类型B类型呢？类型就是一串等长的01串。

也就是说，引入对象这样的概念的意义是：帮助人们左右互看，左看看右看看，外看看内看看。从而和人的左右对齐过去，人也是有左右脑的。

图4
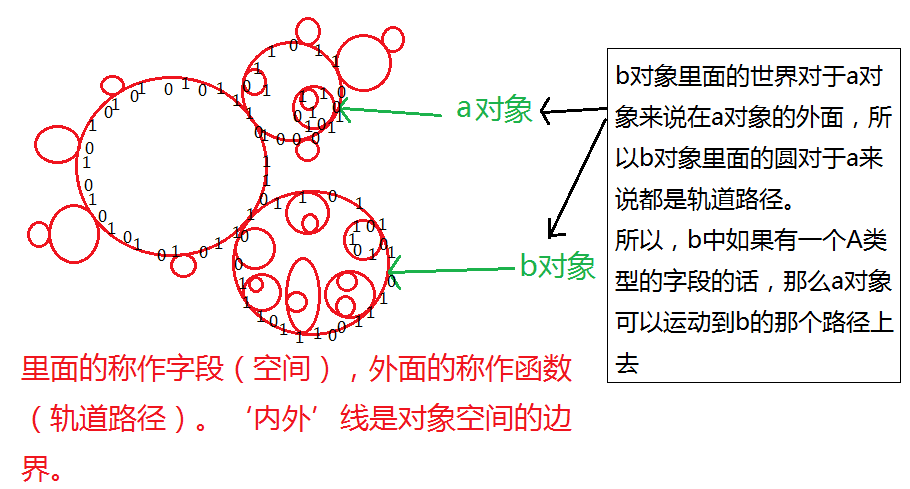
我想在上图的红线上打上01010101……，需要打的太多了，画起来很困难，上图红线上都分布着01，虽然图中有很多接触着的圆，其实它们是一条线绕出来的，用个剪刀剪开个口然后一提溜就知道了，是一条线。

如果b对象中有一串和a对象等长的01串字段空间的话就可以认为b对象中的这个字段是A类型的（光度量长度还不够，暂时忽略上层高维的另外的信息，这里就认为只度量长度就行了）。b中的这个字段能装下去a，所以a能运动到b中的这个字段位置去。
为什么类型，比如int类型是圆形的？因为周期，因为减法是用加法完成的，类型一直都是圆形的钟表那样的周期形的。

感觉如果照这种方法推下去，没有它解释不了的计算机世界。这种方法的优势是它是图形空间运动（集合、树，映射、函数）形的。人的思维离开图形空间后走不太远。

看来字段（空间）和函数（规则、映射、运动定律）是相对的。当A类型中有一个B类型的字段：对于A类型的对象来说它那个相对于它的字段所在的空间位置是字段，但是对于B类型的对象来说却是可以行走过去途经上的路径地点。
时空是一体（本体）的统一的，函数式、命令式是一体（本体）的统一的。
[该贴被anycmd于2016-01-31 22:26修改过]

补上最后一张没有展示出来的图。

生造的词语太多，看不懂。
引用haskell处理IO一句经典的话：计算机模拟是以真实世界为输入，以真实世界为输出的。
指令式只不过是函数式的实例而已。（之前写子集不对，改为实例）
CommandA
CommandB
CommandC
因为指令是带顺序的也就是可以变成
CommandA
()->{
CommandB
()->{
CommandC
}()
}()
这种表达形式甚至可以从变量的生命周期得证：一个变量的生命周期是从变量的声明开始到所在的代码块末尾结束。
而上述形式就是haskell的monad，换句话说指令式的抽象就是monad，或者指令式是一种特殊的monad。指令是特殊函数的计算优先级的纵向表现而已（还不理解的话，可以认为CommandA的返回影响所在代码块在其之后的代码，简单的函数表达形式CommandC(CommandB(CommandA))，monad表达形式是CommandA>>CommandB>>CommandC）

时空概念我就不论，费口舌。
[该贴被SpeedVan于2016-02-25 12:59修改过]
[该贴被SpeedVan于2016-02-28 12:20修改过]

我看不出函数式指令式有什么不同，两者完全一样。都是映射，可能只是映射的单元抽象层次不同罢了。到底是函数式更抽象或还是指令式更抽象也不好说，这要看观察者从哪个方向观察。指令式不是函数式的实例。指令是映射，指令就是把这个东西搬到那个位置把那个东西从那个位置搬过来，“这个东西和那个位置”这是一对映射，直接的映射，如果将“搬”这个运动所耗费的时间丢弃的话（函数概念正是忽略时间丢弃事物的变化而得到的反映映射（也即关系）的概念），这种没有时间的映射就是函数。这跟输入到输出的映射完全是同一个映射。数学老师明确的说过：函数就是映射。指令也是映射，指令和函数没有什么不同，所有的映射最终必定都是空间位置的映射：都是这个空间单元和那个空间单元的映射，为什么必定都是空间之间的映射？因为空间没有时间，空间就是图形，空间就是关系，函数就是图形，所有的数学函数全部都必定可以图形化，如果不能图形化的话那个一定不是函数。
指令和函数到底谁的更抽象，这没法说，这要看观察者从那个角度观察：
public output Func1(input1, input2){
if(input1 > input2) return input1;
return input2;
}
上面这个函数是输入到输出的映射，函数体我认为是又几个更加抽象（比较两个概念哪个更抽象的唯一判断标准是哪个概念涵盖的问题空间更大，哪个更大哪个更抽象，从一个角度看：大小比较、返回值与返回位置等这些指令式概念比Func1更加抽象的多）的映射组成的。
当然，翻过来如果倒着看的话，也可以认为Func1比Func1体中的指令更抽象。我觉得它们两者不是谁是谁的实例的关系。它们两者完全是同一个东西。
[该贴被liangshan于2016-03-14 19:46修改过]

胸中无图无真相，图是空间图是关系，图是空间对应关系，有图可以看图说话。我没有生造词汇，时空概念使我受益匪浅，正是在把握住时空概念后我自感到我几乎能够做到可以随时随地在当时当地的时间与空间使用当时当地的资源面向当时当地的问题空间计算了，自感到我几乎能够精确的读懂任何他人建造的几乎任何上层建筑。我通过联想直接读隐藏在词汇概念下面的时空图形，虽然我能读懂他人，但我不能保证我能够准确的运用上层词汇表达想法，所以几乎从不使用上层词汇，表达问题时我只能用时间和空间去描述问题时空的形状与运动轨迹。

时空思维是对的，爱因斯坦相对论提出时空是相对的，现在我们的时间是不断流逝，也就是不断向前累计的，这是因为我们的宇宙是不断膨胀的，如果宇宙坍缩了，那么时间就会倒流，因此时空其实是一个概念。

在实际中，既然有时间和空间两个区分，那么我们是重视时间还是空间？因为时空一样的，其实目的方向一样，但是区别时间与空间其实是具体路径不同而已。

如果重视时间，那么就是重视逻辑，因为逻辑是时间先后的前后顺序，重视逻辑就是重视计算，重视计算也就是重视CPU与函数。而如果重视空间，或者倾向于空间，那么可能会注重结构，会注重数据。我们知道数据与计算在计算机领域是两个不同的概念，正如数据结构与算法是不同概念一样，算法其实代表计算，代表逻辑，倾向于时间线。

以上只是简单肤浅思考，供参考。

2016-03-14 19:35 "@liangshan"的内容

指令式不是函数式的实例。指令是映射，指令就是把这个东西搬到那个位置把那个东西从那个位置搬过来， ...

你看到monad对指令的实现，你就不可能认为他们是等同的。

x = CommandA；
CommandB(x)；
在指令的角度，x是一个临时存储，他会把CommandA得到的结果存起来。而函数式，认为x是后面monad的参数，且过程并不是x->x，而是>>=（就是bind）,也就是上下CommandA与CommandB之间的组合是可定义。指令式一个不抽象的地方就是把>>=改变成了简单的上下传递x->x。
简单说就是指令式认为x = CommandA中的“=”是CommandA影响之后代码的关键：
CommandA;
=
\x->CommandB(x);
经上述变换，可以发现，真正连接在一起的是因为=号。

monad认为这个是可定义的，加上其他并不屏蔽指令能力（例如那些控制语句，完全可由函数等价实现），这就说monad比指令抽象（反过来就是指令式是monad的实例）。（之前写错的x->x，是想表明，指令对于那个x没作任何处理进行组合）

这足够了？

还得补充一句：有人认为Haskell是现在最好的指令式，也不是没道理的。

[该贴被SpeedVan于2016-03-15 19:47修改过]
[该贴被SpeedVan于2016-03-15 19:48修改过]
[该贴被SpeedVan于2016-03-15 23:55修改过]
[该贴被SpeedVan于2016-03-15 23:56修改过]