贪心算法有时也很有用 - hashnode

贪心算法是解决许多问题的有力武器不幸的是，它们并非总是可行的方法，因为它们可能导致错误的解决方案，它们何时起作用？什么时候是最糟糕的选择？他们什么时候能得出可接受的解决方案？
 
贪心算法尝试通过在每个步骤中采取最佳选择来找到最佳解决方案。您随时可以走一条最大化利己的幸福道路。但这并不意味着您明天会更快乐。
同样，也存在贪心算法无法提供最佳解决方案的问题。实际上，它们可能会给出最糟糕的解决方案。但是在其他情况下，我们可以通过使用贪心策略来获得足够好的解决方案。
在本文中，即使无法保证找到最佳解决方案，我也会写一些贪心算法及其使用方法。
 
贪心算法
贪心算法始终选择最佳的可用选项。通常，它们在计算上比其他算法系列（如动态编程或蛮力）便宜。那是因为他们没有过多地探索解决方案空间。而且，出于同样的原因，他们没有找到解决许多问题的最佳解决方案。
但是，贪心策略可以解决许多问题，而该策略正是最好的解决方法。
Dijkstra算法是最流行的贪心算法之一，该算法以最小的代价找到图中从一个顶点到另一个顶点的路径。该算法通过始终转到最近的顶点来找到这样的路径。这就是为什么我们说这是一个贪心的算法。
这是算法的伪代码。我用G图和s源节点表示。

Dijkstra(G, s):
    distances <- list of length equal to the number of nodes of the graph, initially it has all its elements equal to infinite

    distances[s] = 0

    queue = the set of vertices of G

    while queue is not empty:

          u <- vertex in queue with min distances[u]

          remove u from queue

          for each neighbor v of u:
              temp = distances[u] + value(u,v)

              if temp < distances[v]:
                   distances[v] = temp
     return distances

运行先前的算法后，我们得到一个列表distances，该列表distances是从节点s到节点的最低开销u。
仅当图形的边没有负成本时，才能保证该算法有效。边缘中的负成本会使贪心的策略选择一条非最佳路径。
 
用来介绍贪心策略概念的另一个示例是Fractional Knapsack背包。
在这个问题上，我们有一些项目。每个项目的权重Wi大于零，利润Pi也大于零。我们有一个容量W可观的背包，我们希望以最大的利润来填充它。当然，我们不能超过背包的容量。
在背包问题的分数形式中，我们可以取整个对象，也可以取一部分。当取0 <= X <= 1第i个对象的一小部分时，我们获得的利润等于X*Pi并且需要添加X*Wi到购物袋中。我们可以通过使用贪心策略来解决此问题。我不会在这里讨论解决方案。如果您不知道，建议您尝试自己解决，然后在线寻找解决方案。
 
贪心的时候最糟糕
在上一节中，我们看到了使用贪心策略可以解决的两个问题示例。这很棒，因为它们是非常快的算法。
但是，正如我所说，Dijkstra的算法不适用于带有负边的图形。而且问题甚至更大。我总是可以用Dijkstra的解决方案达到我想要的效果来构建带有负边缘的图形！考虑以下示例，该示例是从Stackoverflow提取的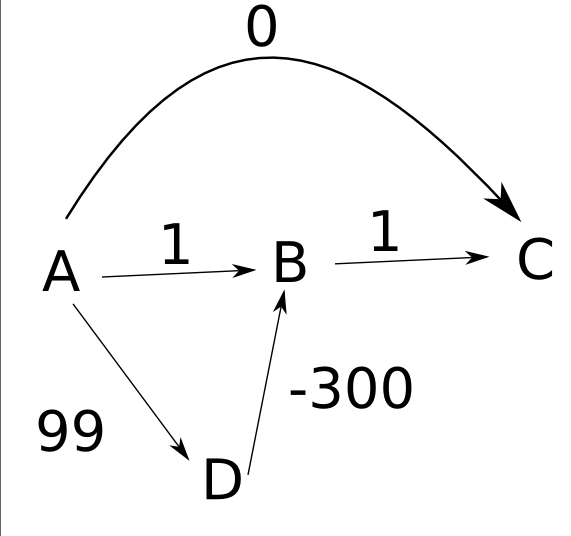

Dijkstra算法未能找到之间的距离A和C。查找d(A, C) = 0何时应为-200。并且，如果减小edge的值D -> B，我们将获得一个距离实际最小距离甚至更远的距离。
类似地，当我们无法在背包问题（0-1背包问题）中破坏对象时，使用贪心策略获得的解决方案可能会像我们想要的那样糟糕。我们总是可以为使贪婪算法严重失败的问题建立输入。
 
另一个例子是旅行者问题（TSP）。给定一个城市列表以及每对城市之间的距离，最精确的路线是什么？
我们可以总是去最近的城市来贪心地解决问题。我们选择任何一个城市作为第一个城市并应用该策略。
正如前面的示例中所发生的那样，我们总是可以通过贪心策略找到最糟糕的解决方案的方式来构建城市。
在本节中，我们看到了贪心的策略可能导致我们陷入灾难。但是存在一些问题，其中这种方法可以很好地逼近最佳解决方案。
 
贪心的时候还不错
我们已经看到，贪心策略对于某些问题来说是我们想要的那样糟糕。这意味着我们不能用它来获得最优解，甚至不能很好地近似它。
但是，在某些示例中，贪心算法为我们提供了很好的近似值！在这些情况下，贪心方法非常有用，因为它往往更便宜且更易于实现。
图的顶点覆盖是最小的一组顶点，以使图的每个边缘在该集中具有至少一个端点。
这是一个非常困难的问题。实际上，没有任何有效且精确的解决方案。但是，好消息是我们可以使用贪心算法进行近似。
我们<u, v>从图中选择任何边，然后将u和添加v到集合中。然后，我们删除所有具有u或v作为端点之一的边，并在其余图具有边的同时重复上一过程。
这可能是先前算法的伪代码。

vertexCover(G):
    VertexCover <- {} // empty set
    E' <- edges of G

    while E' is not empty:
          VertexCover <- VertexCover U {u,v} where <u,v> is in E'
          E' = E' - {<u, v> U edges incident to u, v}

     return VertexCover

如您所见，这是一个简单且相对较快的算法。但是最好的部分是解决方案将始终小于或等于最佳解决方案的两倍！无论输入图的构建方式如何，我们都永远不会获得大于较小顶点覆盖范围两倍的集合。
我不会包括在这个帖子这句话的示范，但你可以注意到，每边证明这一点<u, v>，我们添加到顶点覆盖，无论是u或者v是最佳的解决方案（即在较小的顶点覆盖） 。
许多计算机科学家正在努力寻找更多这些近似值。还有更多示例，但我将在这里停止。这是计算机科学和应用数学领域一个有趣而活跃的研究领域。通过这些近似值，我们可以通过实施非常简单的算法来为非常棘手的问题提供非常好的解决方案。