多维思考是超越二维思考的非线性概率思考模型,多维分析三步过程:
- 步骤 1. 确定关键维度,
- 步骤 2. 构建多维模型,
- 以及步骤 3. 分析模型以形成合理准确的结论。
步骤1中:确定关键维度不是二分法:黑与白、好与坏、阴与阳,例如,在决定是否投资一家公司时,我们需要确定可能影响公司未来的关键因素。对于星巴克来说,这可能是他们在中国的持续扩张。对于亚马逊来说,它可能是 AWS 和 3'rd 方零售的未来。
步骤2中:建立多维模型。例如,我们构建了一个马尔可夫链,它捕获了我们问题的所有关键方面。培养对各种此类心智模型的流畅性是关键。更多模型=更多工具,我们必须准确反映我们的情况。
步骤3中:分析模型以形成合理准确的结论。它也有助于熟悉各种分析。在商业和投资方面,我们的“分析工具箱”可能应该包括 DCF、反向 DCF、蒙特卡洛方法、单位经济学和 LTV vs CAC 分析等。
马尔可夫链
在生活和投资中,我们经常遇到运气/机会起着重要作用的情况。马尔可夫链通常是对此类情况进行建模和分析的好方法。
案例:假设我们有2个志愿者:Alice 和 Bob。我们给他们每人一枚公平的硬币。我们要求Alice持续抛硬币,直到她看到正面然后下一次紧跟其后的是反面(即模式 HT)。Bob也是持续抛硬币,直到他看到两个连续的正面(即模式 HH)。
问题是:平均而言,谁会花更多的时间来达到他们的“目标模式”?还是他们平均投掷的次数相同?
更准确地说:假设 Alice 平均投掷 A 次来获得她的 HT。鲍勃平均投掷 B 次才能得到他的 HH。那么,谁的数字更大:A 还是 B?还是他们都是同一个数值?
我们知道 Alice 和 Bob 都有公平的硬币。因此,在任意 2 次连续抛掷中,Alice 的 HT 出现的可能性与 Bob 的 HH 一样。因此,平均而言,*似乎*他们都会进行相同数量的抛掷(即,A = B)。
但这不是正确的答案。正确答案是:平均而言,Alice 的 HT 只会出现在 4 次抛掷中。但是鲍勃的 HH 需要掷 6 次。也就是说,A = 4 和 B = 6。Bob 平均需要更长的时间。
多奇怪!?
情是这样的:当谈到概率时,我们的直觉经常把我们引入歧途。处理它的最好方法是精心写下各种可能的结果,并实际进行数学计算。马尔可夫链是实现这一目标的便捷模型。
例如,这里是 Alice 的马尔可夫链。它表明,在任何时候,Alice 都可以处于 4 种可能的“状态”之一(S0 到 S3)。在每个状态,爱丽丝抛硬币。并且根据抛掷的结果(H 或 T),如果需要,她会移动到不同的状态。

S0 是“开始”状态。这是Alice开始她抛硬币起点。在 S0,Alice 抛硬币。如果出现硬币正面,她会跟随S0后面(标记为“H”)的橙色箭头,将她带到 S1状态。
在 S1状态,Alice 看到了正面,并希望接下来看到反面(所以她有她的 HT 模式)。如果她在 S1 的投掷出现了反面,她将进入 S2——她的胜利状态;HT 模式实现了。但是如果它还是出现正面,她会跟随 S1 的下面橙色箭头,这让她保持停留在 S1 状态。
这就是马尔可夫链的全部内容。有一堆状态。在每个状态,都会发生一个随机事件(如抛硬币)。根据这个随机事件的结果,我们按照适当的箭头进入下一个状态。一旦进入下一个状态,我们不断操作。
下面是这是Bob的马尔可夫链。Alice 和 Bob 之间的区别现在很清楚了。当 Bob 在 S1 并且不走运(带有 T)时,他必须“回到零”(S0)并重新开始。爱丽丝不是这样。一旦 Alice 在 S1,她就永远不必回到 S0。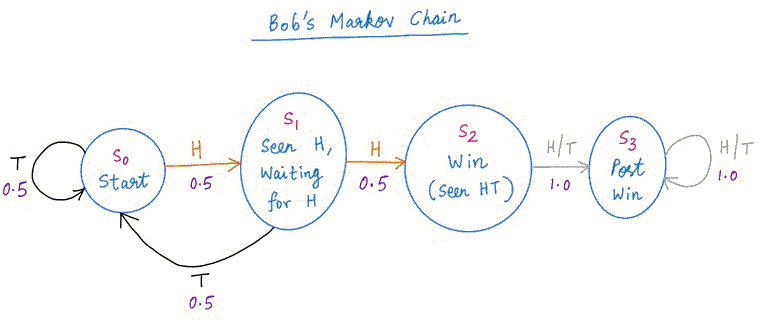
这就是为什么Bob需要更长的时间!有时,他与Alice不同,Bob被迫从零重新开始。那是一个拖累。爱丽丝就像一个醉汉,要么原地不动,要么勇往直前。但鲍勃就像一个醉汉,偶尔也会*向后*。
马尔可夫链的好处在于它们允许我们量化所有这些。如果我们知道初始状态(Alice 和 Bob 的 S0),我们就可以计算在 *任何*时间处于*任何*状态的概率。对此有一个简单的公式。
马尔可夫链公式
这个公式是“迭代的”。也就是说,如果我们知道在时间“k”(即,在“k”次抛硬币之后)处于每个状态的概率,则公式为我们提供了在*下一个*时间“k+1”每个状态的概率(即,在“k+1”次抛硬币之后)。
这很简单。我们取时间“k”的概率,然后将它们预先乘以一个矩阵(称为马尔可夫矩阵或转移矩阵)。这种乘法为我们提供了时间“k+1”的概率。这是 Alice 和 Bob 的马尔可夫矩阵。为了得到这些矩阵,我们只需取每个马尔可夫链“箭头”的概率,并根据箭头的“From”和“To”状态将其放置在适当的矩阵槽中。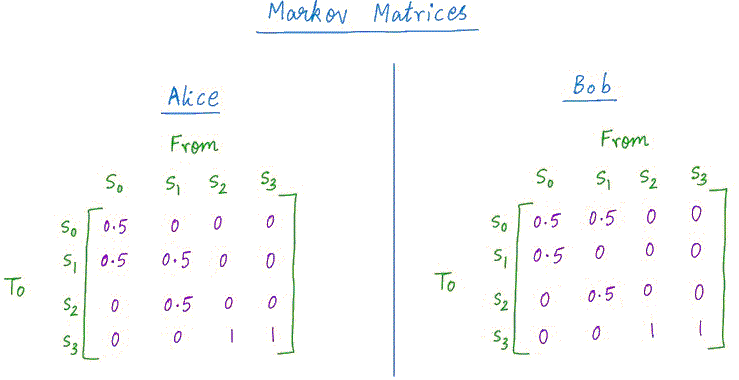
现在,我们可以迭代了。使用重复的马尔可夫矩阵预乘,我们得到 Alice 和 Bob 在每个可能的时间处于每个可能状态的概率。像这样(对于时间 0 到 4):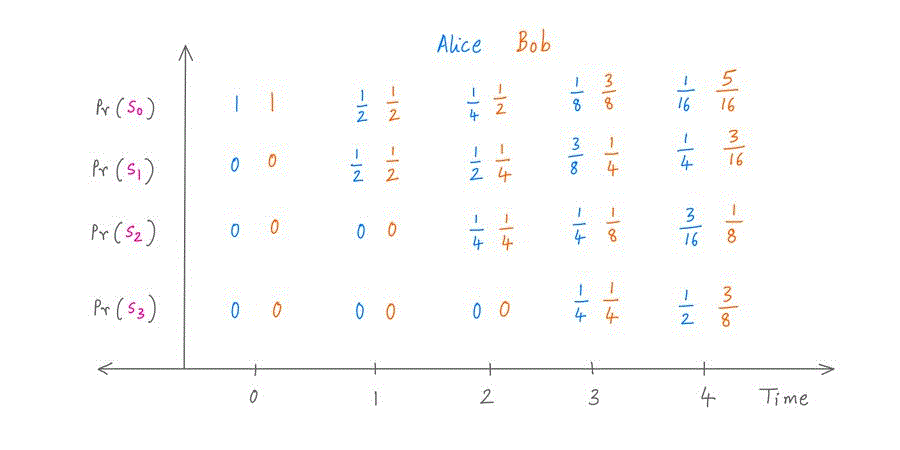 在任何时候,如果 Alice 或 Bob 看到了他们的目标模式,他们就会在 S2 或 S3 中。所以,我们可以看到,在 4 次抛硬币之后,Alice 已经有 Pr(S2) + Pr(S3) = 3/16 + 1/2 = 68.75% 的机会完成。但是到那时,Bob 只有 50% 的机会完成。
在任何时候,如果 Alice 或 Bob 看到了他们的目标模式,他们就会在 S2 或 S3 中。所以,我们可以看到,在 4 次抛硬币之后,Alice 已经有 Pr(S2) + Pr(S3) = 3/16 + 1/2 = 68.75% 的机会完成。但是到那时,Bob 只有 50% 的机会完成。
获得*平均*的完成时间也不难。由于“在时间 k 完成,但不是在时间 k 之前完成”与“在时间 k 处于状态 S2”相同,我们有以下内容: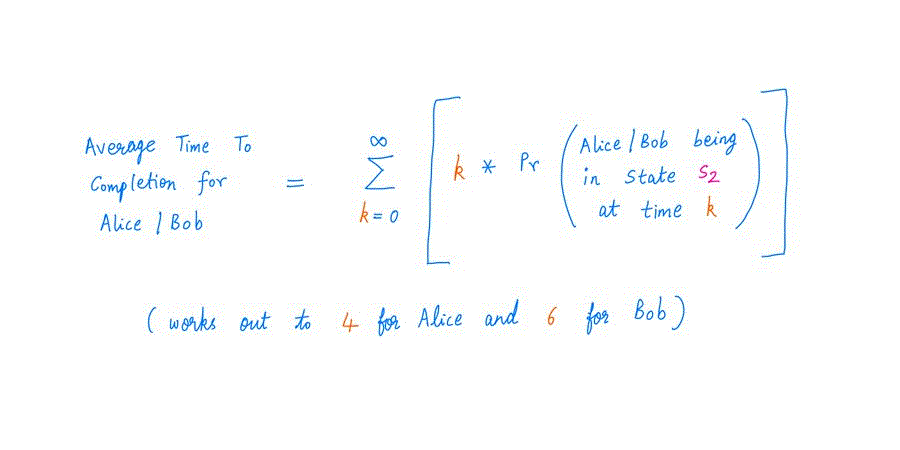
所以,这就是马尔可夫链的基本数学。太简单了。我们根据抛硬币等偶然事件的结果从一个状态转移到另一个状态。而且如此强大。只知道初始状态,我们就可以准确地计算出在 *任何*时间处于*任何*状态的概率。
关键教训:
首先:机会和不确定性在生活中无处不在。因此,重要的是学习如何正确地推理概率情况——使用系统的数学技术,*不*依赖我们的直觉。
关键教训 2: 我们应该尽可能避免让自己陷入一次厄运就可能迫使我们从零开始的情况。这是鲍勃的问题。这就是为什么在我们的例子中他比 Alice 花费的时间更长。
在投资中,相当于使用过多的杠杆、裸期权、保证金交易等。通过做这些事情,我们将自己置于短期波动和偶然事件可能会消灭我们的位置,迫使我们基本上一切从零开始。
关键教训3: 熟悉“经典”很重要——来自多个学科的伟大思想。马尔可夫链并不新鲜。它们的历史可以追溯到 1906 年。但直到今天,它们仍被大量用于各个领域——从工程到生物学。
这类经得起时间考验的经典思想,往往值得研究。它们经常帮助我们更清晰地思考——从而更好地了解世界。正如查理芒格所说,它们是添加到我们的“心智模型网格”中的好选择。