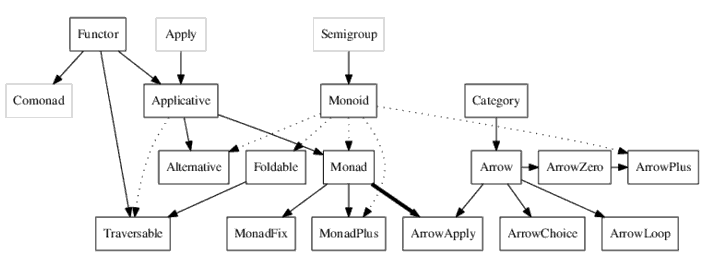
什么是群group和monad？

这是来自数学家背景的大牛通过以时钟为比喻形象解释了群论和函数编程中的一些抽象概念，如Monoid、Monad等等。

群论是一种代数结构，这个结构是带有元素的集合set，但不是一般普通集合，而是带有操作的集合，通俗讲是：集合+操作。难点就是关于这个操作，首先这个操作定义是什么？是结合两个元素产出第三个元素，而且这个操作必须满足方程法则。

那么怎么理解方程？什么是方程法则，也就是数学中解方程的方程，这里大牛做了一个比喻，用时钟算术做比喻，脑海里浮现一个挂钟或手表，一个时钟是由12个小时组成，用这个12小时循环往复。

首先，给任何一个时刻增加时间都不会超过这个12小时循环，这就是结合两个元素产生第三者结果时间还是处于12小时这个闭环中；属于Closure。

其次，时间增加总是平均向前，不增加任何时间，它还停在原处。同时也有时间反演对称性，前进几步，退后几步，还是回到原来的时间点。

精确用四个法则总结如下：假设有一个集合定义为G，和集合的操作定义为(G,*)：

1.闭环Closure：对于G中所有a,b元素，a*b的操作结果也是在G中。

2.可结合性Associativity：对于G中所有a,b元素，(a⋆b)⋆c=a⋆(b⋆c)，这个相等性在我们解方程时是经常用到的，不过经常用x y z取名，以加法操作为例，(x + y )+ c = x + (y + c) 。

3.单位元Identity：对于G中任何元素a，有一个元素e，e⋆a=a⋆e=a. 也就是说，有一个元素e和G中任何元素操作，无论操作顺序如何，结果还是a。时钟中对于任何时间点增加任何时间间隔，结果还是一个时间点，如果时间间隔是空的或无，那么停留在原来时间点，这个空无的元素也称为单位元或幺元。

4.可逆性Invertibility：对于G中每个元素a，有一个元素b，还有一个单位元，那么a⋆b=b⋆a=e。以正反函数为例，y=3x+5，其反函数是y=(x-5)/3，这两个正反函数是恒等的。

所以，群group是一个带有操作并满足于closure, associativity, identity 和invertibility这四大法则的集合。

群论是下一代用于互联网交易和银行安全算法椭圆曲线密码学（elliptic curve cryptography，简称ECC）的重要概念。也是维格纳定理（Wigner's theorem）或时间反演对称性的基础。

函数式编程本质上属于群论或范畴论，monoid也是一种群group，它满足的法则：
1.左恒等：mempty <> x = x
2.右恒等：x <> mempty = x
3.可结合性：(x <> y) <> z = x <> (y <> z)

由此可见：monoid好像不是一种首尾相连的如时钟一样的环，而是有头有尾，它是可追加Appendable的集合，因此monoid是个半群，而Monad则又是一种特殊的monoid。

[该贴被banq于2016-05-23 15:25修改过]