很多人认为数学家喜欢数字。然而,这并不完全正确。数学家 喜欢精确、清晰,最重要的是,他们喜欢理解结构。人们将数学与数字联系起来的唯一原因是因为我们喜欢量化事物。但对普通大众来说不太清楚的是,我们量化不是为了好玩,我们量化是为了理解、组织、定义。
附加到数学概念上的数值有助于我们更好地理解该概念。它们还帮助我们将具有相同或足够相似属性的事物组合在一起。例如,如果我们看一个三角形,其中两条边等于 7 厘米,第三条边等于 12 厘米,我们可以立即说它属于等腰三角形。
当我在写博士论文时,我哥哥看到并惊呼——“数字在哪里?这只是文字和奇怪的字母!”。我认为“奇怪”是指在页面上写的大多数方程式中出现的所有希腊字母。
我们深入数学的海洋越深,我们看到的数字就越少。
这是因为数学实际上是在解释一般现象。数学家使用的字母被称为“变量”,顾名思义,它们可以取不同的值,它们“变化”。在主要由字母定义的表达式中插入不同的数字会产生新的例子。用数值计算各种例子对于发现一般现象背后的趋势和形成所谓的猜想非常有帮助。
也许这有点违反直觉,但是将某些东西剥离到其骨架上,并仅将其作为抽象结构进行研究,这通常会揭示隐藏的属性,并有助于更深入地了解所讨论的对象。
例如,我们知道我们有整数、有理数、实数、复数和四元数。当我们查看每组具有哪些潜在性质时,我们推断所有这些在二元运算加法和乘法下都是封闭的,它们在减法下都是可交换associative的和封闭的closed ,但整数在除法下不是封闭的,四元数不是可交换的(即我们在四元数中将两个数字相乘的顺序很重要——如果我们将数字轮换,我们会得到不同的结果)。
因此,当我们放眼大局并尝试分离特定属性时,我们会看到研究对象的真实结构。
在许多其他方面,着眼于更大的图景使我们能够做到以下几点:
- a) 深入研究对象的结构;
- B) 在这个对象和其他对象之间建立意想不到的连接。
例如,整数形成一个环。环是抽象代数中的基本对象,并且已经研究了几十年,如果不是几个世纪的话。因此,通过发现整数是环,我们可以使用我们所知道的关于环的理论,并更多地了解整数的性质,而无需对它们进行任何实际具体的进一步研究。
这或多或少是范畴论的产生方式和原因。它提供了数学对象结构的鸟瞰图。它是一种新的通用语言,允许我们同时谈论数学的多个领域。它使我们能够在看似无关的研究领域之间建立许多桥梁,从而发现许多意想不到的联系,从而导致非常富有成效的研究。
范畴论是数学的一部分
它为我们提供了讨论和探索结构所需的工具。它是一种组织工具、记账资产、地图、日记、日记。它记录并连接。它就像洞穴中的火炬——乍一看是一个简单的发明,让我们对地表之下的事物有了深刻的了解。
范畴论的美妙之处在于剥离所有细节,深入研究我们所研究的事物的底部,它揭示了基本的骨架。它有两种工作方式——你可以尝试在范畴论框架中工作,然后将发现应用于不同的数学领域,或者尝试将特定结构的已知属性翻译成范畴论语言,看看这会揭示什么。它为从一般到具体,反之亦然铺平了道路。
范畴论基础知识
一个范畴category由两部分组成:对象和态射。
对象是我们想要考虑的元素,态射是它们之间的映射。映射也满足一些标准条件,例如,我们可以“组合”它们,或者用人的话来说,将它们组合起来。
例如,范畴的第一个很好的例子是有限集的范畴,称为Set。对象是有限集,态射是这些集的映射。Set是元素的集合,例如,集合 {1,2,3} 是 3 个元素的集合,其中每个元素都是一个数字。集合中元素的个数就是集合的大小。所以我们的例子 {1,2,3} 是一个大小为 3 的集合。
集合之间的映射是一种赋值,它将一个集合的元素发送到另一个集合的元素。如果我取集合 {1,2,3} 和 {4,5,6,7,8},我可以定义一个发送 1 到 5、2 到 7 和 3 到 4 的映射。注意定义集合的映射你不必从相同大小的集合开始。
So the structure where objects are sets and morphisms are maps of sets defines the category Set of finite sets.
对象的结构是集合set,而morphisms 是定义这些集合之间的各种映射,通过研究这个抽象定义的结构,我们可以推导出关于对象和态射的新属性。我们可以将它们连接到具有不同对象和态射的范畴。
两个范畴之间的映射称为函子,然后我们可以研究两个范畴之间的不同种类的函子,我们可以组合函子。我们甚至可以研究函子之间的函子,称为自然变换natural transformations,等等。可能性是无穷无尽的。
...点击标题见详细
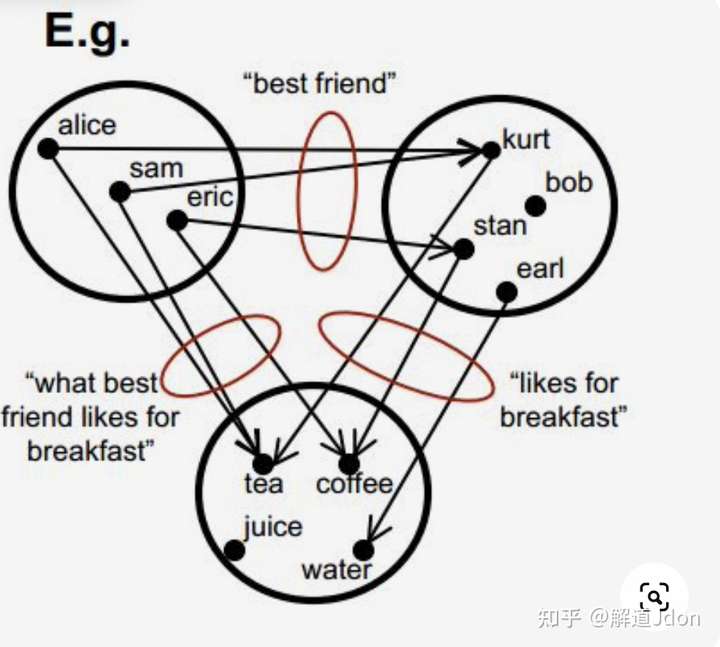
举例:我们这里有三个独立的范畴:女孩的范畴,称之为女孩们;男孩范畴,称之为男孩们,还有一类饮料范畴:饮料们。由于所有这些都是离散的,我们在范畴内没有任何关系——即,我们假设没有任何女孩之间有任何关系,男孩和饮料也是如此。然而,我们在范畴之间有关系——即函子。
有一个从女孩们到男孩们的函子,由映射关系“最好的朋友”给出定义,还有一个从男孩们到饮料类的函子,由“喜欢早餐”给出定义。
现在请注意,要获得从女孩们到饮料的函子,我们可以先按照女孩们到男孩们态射箭头,然后按男孩们到饮料的态射箭头。因此,这个函子是这些函子组合的一个例子。这就是它被称为“最好的朋友喜欢什么早餐”的原因。
范畴论为我们提供了一种研究各种事物的新语言。它为我们提供了一个统一的环境,适用于数学的各个领域,而不是研究特定的案例,通过研究某个类别,我们可以同时研究多种事物。
这个想法是革命性的,在物理学、计算机科学、编程、语言学、语言研究,当然还有数学本身有很多应用。范畴论本身是一个有趣的学科,但最令人兴奋的部分是它展示了数学的不同领域实际上是如何相互关联的,并给出了将学科作为一个统一的整体而不是看似分散的集合的新视角。不同的话题。