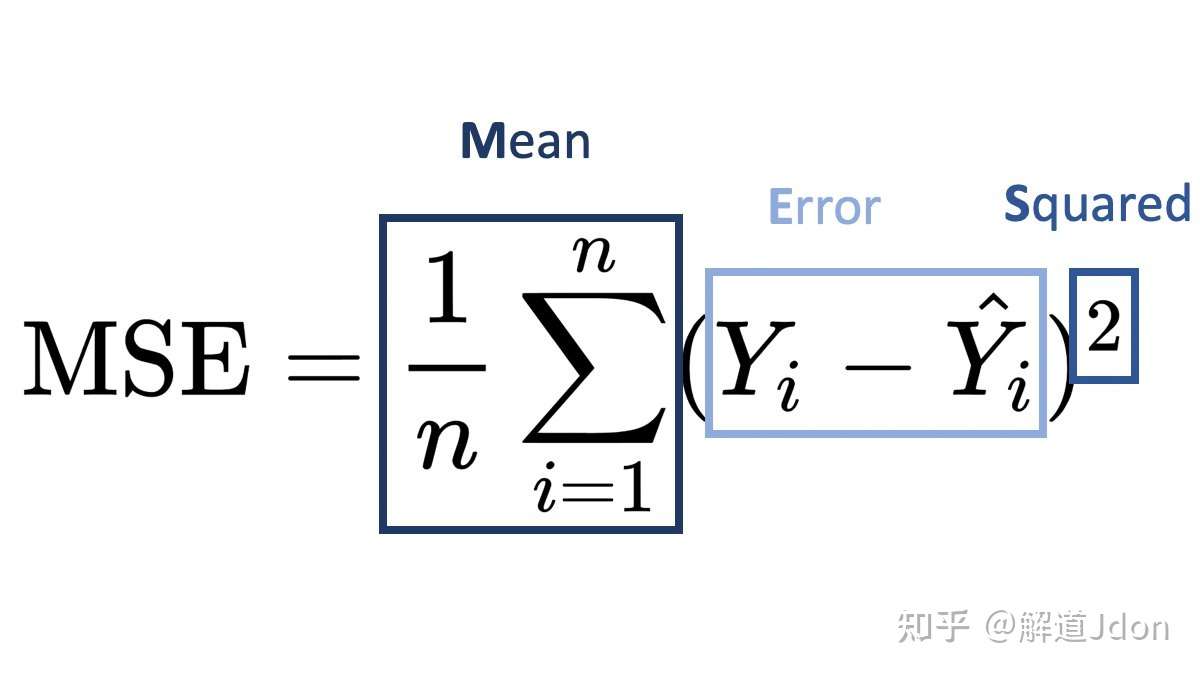
均方误差 (MSE)是用来测量预测值Ŷ与某些真实值匹配程度。MSE 通常用作回归问题的损失函数。例如,根据其属性估算公寓的价格。
详细公式解释
均方误差公式可以写成如下,它代表了一个非常简单的概念,但如果您刚开始使用 ML,可能不太容易读懂。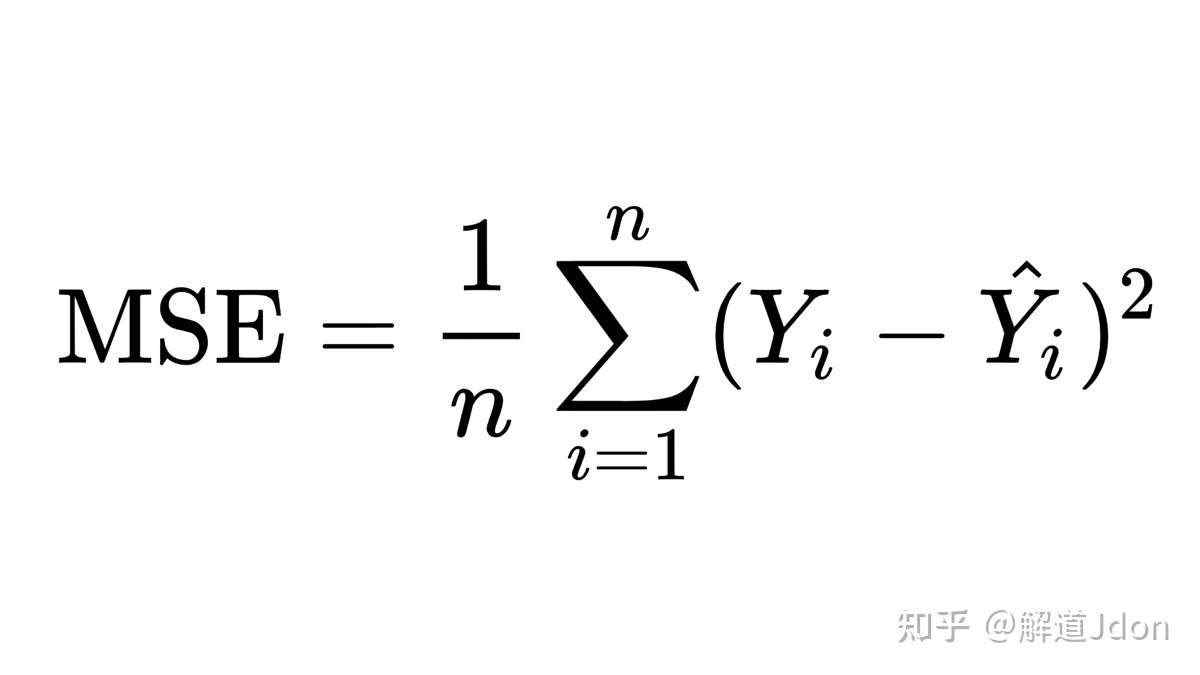
误差被定义为预测值Ŷ和一些真实值之间的差异Y。例如,如果您要预测房价,则误差可能是预测价格与实际价格之间的差异。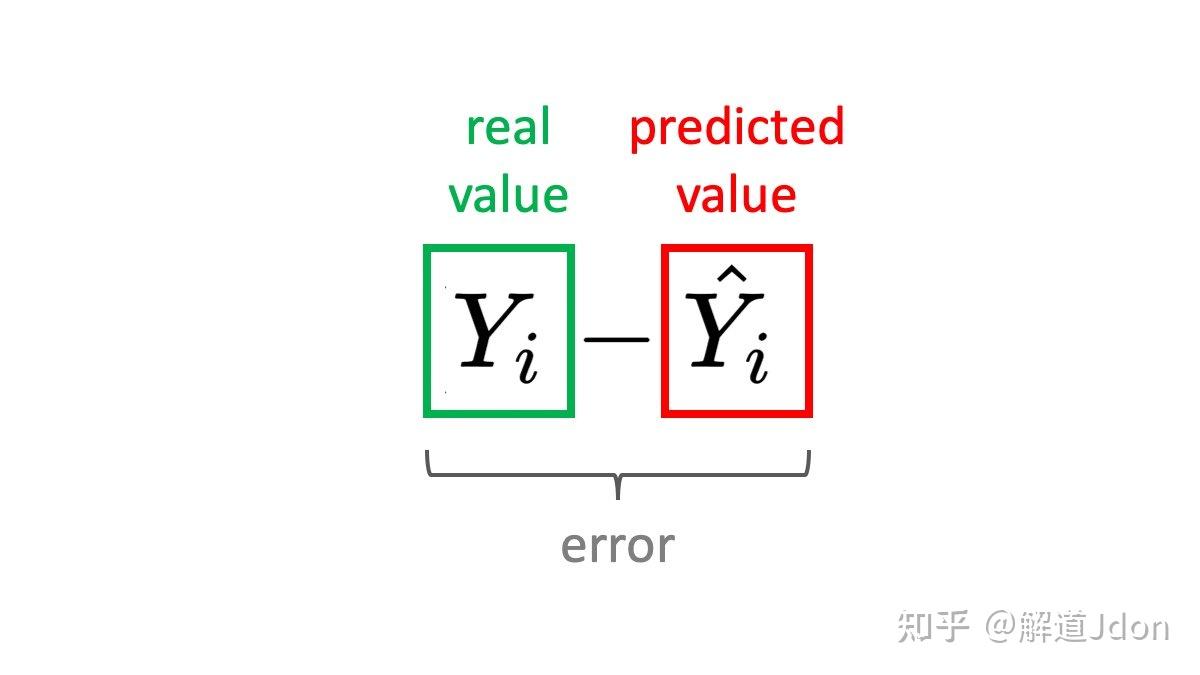
从标签中减去预测是行不通的。误差可能为负也可能为正,这是对样本求和时的问题。想象一下你对两套房子价格的预测是这样的:
- House 1:实际 120K,预测 100K -> 错误 20K
- House 2:实际 60K,预测 80K -> 误差 -20K
如果你总结这些错误将是 0,这显然是错误的。要解决这个问题,您可以取绝对值或误差的平方。正方形有一个特性,它惩罚更大的错误更多。使用绝对值将为我们提供另一个流行的公式 - 平均绝对误差。
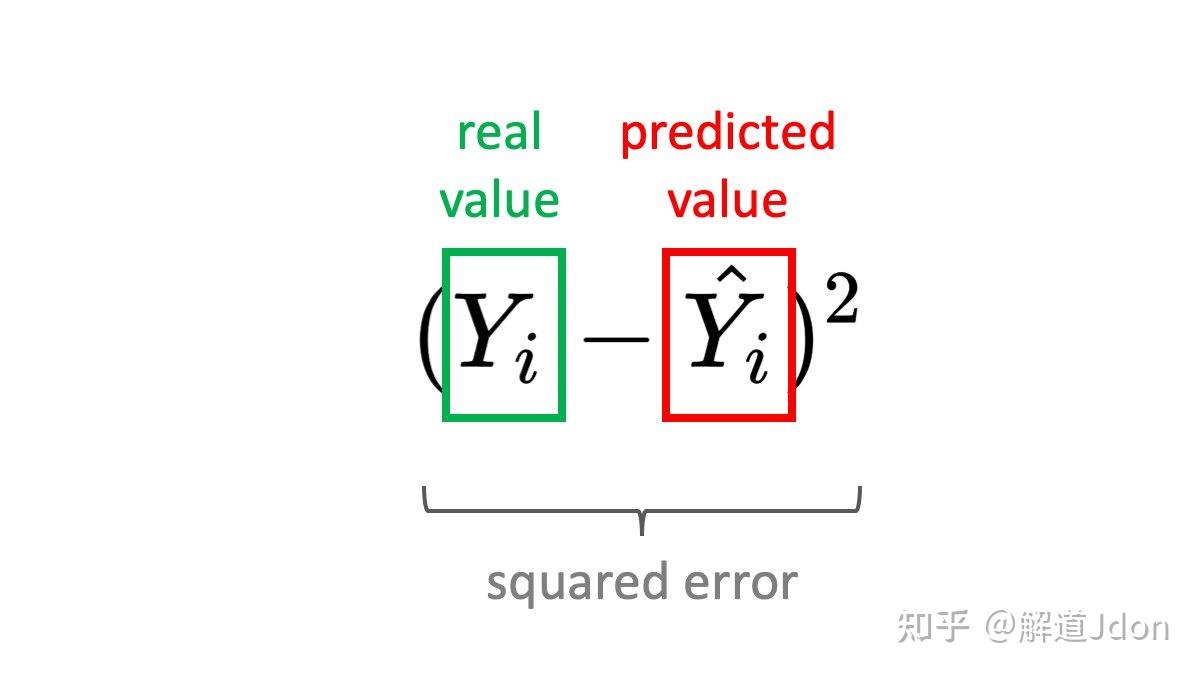
我们通常计算多个样本的误差(在我们的例子中 - 房屋)。这是训练机器学习模型时的典型情况 - 您的批次中将有许多样本。我们需要计算每一个的误差并求和。同样,在这里让误差始终≥ 0 很重要。
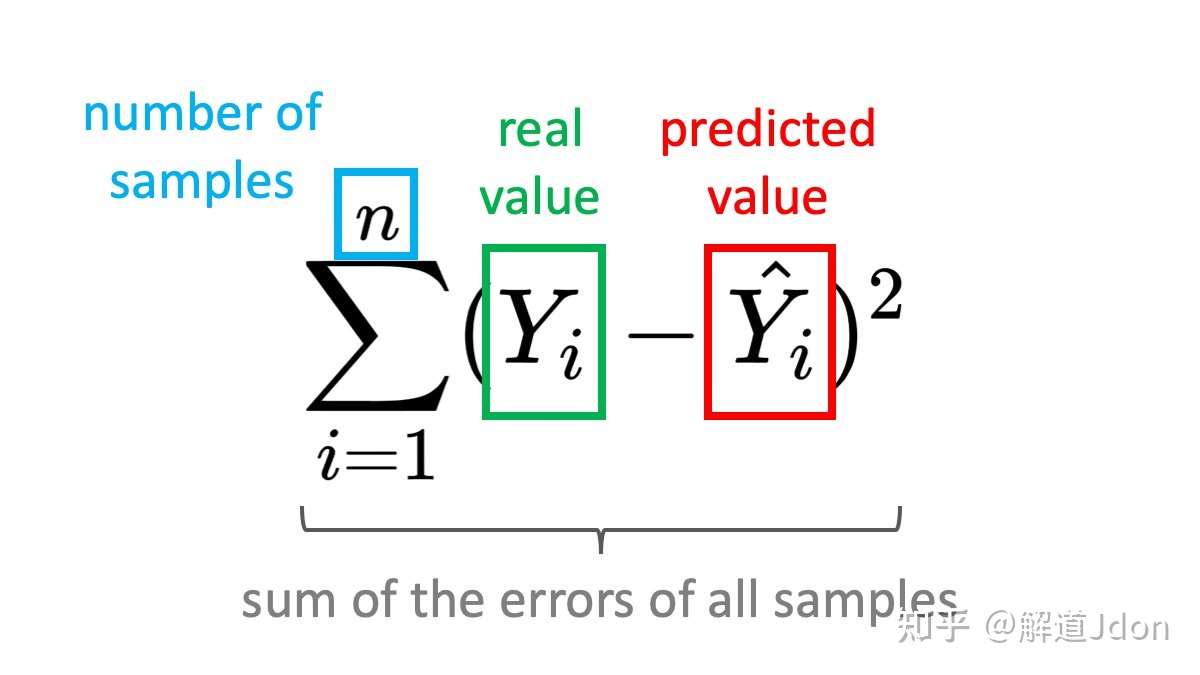
如果要比较不同大小批次的误差,则需要对样本数量进行归一化——取平均值。例如,您可能想查看哪个批次大小产生的误差较小。

现在应该更容易理解公式了!MSE 是 ML 回归模型(例如线性回归)中常用的统计度量和损失函数。您还应该查看平均绝对误差 (MAE),它可以更好地处理异常值。