函数式编程模式:半群Semigroup
函数式编程中一个重要概念是组合, 一个聚合体或复杂元素是由很多小部分组合而成。但是不是所有的组合形式是一样的,看看下面两个情况:
- 拼图游戏的拼图组装
- 组装一个宜家家具
这两个组合不一样的,家具组合是高度线性和顺序的,一般来说,按照手册第一页开始第一步,遵循顺序直至到最后。而拼图游戏的组合更自由,可以从左上角开始,也可以从右下角开始,拼图工作很容易同时进行,你和朋友可以分别从不同地方开始拼图,最终汇合。
我们是否可以通过代数来描述这两种情况?拼图组合满足下面条件:
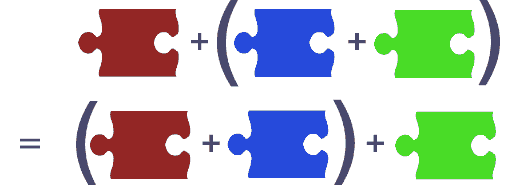
对于三块拼图,你能以两种不同方式放在一起,第二块和第三块或者第一块和第二块,无论哪两种组合方式,最终结果是相同的。如下图:

组合方法如果满足上述这种约束可以称为associative(可联合的 可结合的),拼图是遵循可联合的法则,这种法则不断被重复应用,直至拼图以任何一种顺序被组装起来。
定义
一个半群Semigroup 是一种带有组合方法的数据类型,组合符合是:⊕,组合方法满足可联合的法则:
a ⊕ (b ⊕ c) = (a ⊕ b) ⊕ c
案例
带有加法的数字是半群的,数字有最大值和最小值,这代表另外一种概念单位元(Identity element),带有一个指定代数类型的同样数据类型可以有多种方式:
a + (b + c) = (a + b) + c
a * (b * c) = (a * b) * c
max(a, max(b, c)) = max(max(a, b), c)
min(a, min(b, c)) = min(min(a, b), c)
带有字符串连接的字符串可以形成一个半群,用++表示连接,"foo" ++ "bar" = "foobar",表达式:
a ++ (b ++ c) = (a ++ b) ++ c
类似带有列表/数组连接的集合和数组也是半群,用++表示列表或数组连接操作,表达式表现为:
[1, 2] ++ [3, 4, 5] 等同于 [1, 2, 3, 4, 5]
带有||和&&的布尔值也是半群:
a && (b && c) = (a && b) && c
a || (b || c) = (a || b) || c
一个重要联合操作是函数组合:
f ∘ (g ∘ h) = (f ∘ g) ∘ h
矩阵乘法是一个二进制将线性函数构成的行为编码的操作,因而也是联合的,能制作nxn矩阵的半群。
一个频率map是带有频率的map,频率代表一个数字在时间次数,在选举中可以用这个表达投票次数,候选人的选票次数的频率map如下:
{ A: 2, B: 4, C: 3, D: 1 }
简单操作是将频率进行相加:
addFrequencies({ A: 2, B: 1, C: 3 }, { B: 3, C: 1, D: 5 }) >> { A: 2, B: 4, C: 4, D: 5 }
这个操作对于所有数值都是可联合的,选举结果是并行计算问题的一个典型的例子。没有一个人在一次选举中计算出所有选票,而是将结果按照区汇总,汇总完成最后完整的结果。
比较器是半群,一个比较器是将两个值进行比较的函数:
function compareNumbers(i, j) { return i - j; }
按照右偏比较的顺序组合两个比较器变成一个新的比较器,比如firstNameComparator ⊕ lastNameComparator 是按照其lastName比较然后再按照firstName比较:
function composeComparators(c, d) {
return (x, y) => {
const comparisonResult = d(x, y);
if (comparisonResult === EQUAL) {
return c(x, y);
}
return comparisonResult;
};
}
一个奇怪的联合操作是 +)
x +) y = y
这是将两个参数去掉第一个,任何带有此操作的类型都是半群。
带有半群参数对组成的集合也是半群,(4, "foo") ⊕ (7, "bar") = (11, "foobar")