函数式编程模式：单位元(幺元 Identity Element)

　　单位元(又称幺元，英文Identity Element)是代数和函数式编程中常见的模式，它实际就是关于空的定义，是不是有点像老子道德经中的“无”“空虚”。

有一些确定的值 -可能散落在你现在正在工作的代码中 - 像数字1和0的一些值，空字符串""或空数组[]，，这些空值经常用来实现初始化，是某种“空”的意思或没有任何意思。

单位元模式允许我们能以精确的方式将这些符号正式化。

想象一个空杯子，如何定义杯子是空的呢？日常生活或非正式场合很容易做到，但是从抽象角度思考，如何使用一个正式属性表达空杯呢？相对于不是空的杯子。

关键这里是定义一个附加操作来结合两种杯子，我们称为这个操作为“倒”，取出两个杯子，倒出里面的东西进入一个新的完全相同的容器中。

现在完成下面的操作如图，我们发现一个属性被完成：倒出空杯的内容进入另外一个杯子，留下另外一个杯子不变。

同样，将任何一个杯子倒出内容到这个空杯。

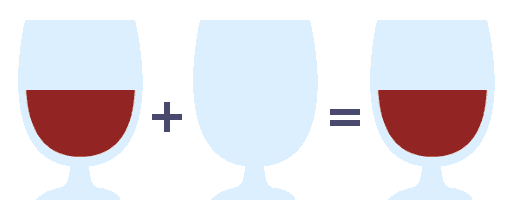
正式情况下，我们将这两个操作写如下代码，这里x代码任意杯子：

pour(emptyGlass, x) = x  
pour(x, emptyGlass) = x

我们使用其他空值来验证看看，比如数字0，我们假设这个操作是add，就是将两个数字加在一起，比如add(3,9)=12，那么代码如下：

add(0, x) = x  
add(x, 0) = x

这个0实际代表空，这样这个0是一个单位元，相对于我们的操作add。

同样在一个钟表时间内，用0-12小时表示时间，任何一个空时间也就是时间不增加也不减少，钟表时针也就停在原地不动，所以，这里空时间也是一个幺元或单位元。

再看看空数组，假设操作的合并数组concat，concat("foo", "bar") = "foobar"或concat([1,2,3], [4,5]) = [1,2,3,4,5]，那么代码如下：

concat("", x) = x  
concat(x, "") = x

并且：

concat([], x) = x  
concat(x, []) = x

空数组和空字符串相对于合并操作来说是单位元，这样这些空能被正式描述。

通常情况下，一个集合A带有一个封闭操作 ⊕,一个空(identity)元素e是A中一个元素，这样，对于A中所有的x，我们有：

x ⊕ e = x  
e ⊕ x = x

我们可以到处寻找到单位元的例子，他们是很常见的，大量的隐藏在各个地方。让我们看更多的案例。

首先看看数字领域，有一个特殊值：无限大，∞，无限大看上去是空的反面，但是它也是一个单位元的案例，如何精确描述无限大是数字的空元素呢？

为了理解这个问题，可以想象一下上界，假定有一句语句：房间里最老的人是80左右的老人，这相当于定义了房间内人们年龄的信息，一种表达式是：房间内最老的人是几乎是∞年龄了。

无限大作为上界，没有传递任何信息，因此在这个意义上是空的，我们选择什么符号表示这个概念呢？答案是使用min操作：

min(∞, x) = x;  
min(x, ∞) = x;

如果你愿意，可以试试负无穷大，选择合适操作证明它是空的。

现在看看多个空对象也许可以存在，配以不同操作以给予对空虚的某种理解。另外一个值是1带有操作mul，比如mul(5,3)=15

mul(1, x) = x;  
mul(x, 1) = x;

这种对空性的解释是自然的。

另外一个重要案例是单元函数(identity function)，如(X=>X)，或经常被称为id，单元函数是是一种将输入没有改变输出的函数，比如id(3)=3或id(x)=x

我们可以选择什么样的操作能看到这是一个单位元呢？这种操作通常是两个元素的自然组合方式，这样选择函数组合就是答案了：(f, g) => x => f(g(x))，或者经常被写为类似句号字符∘ ,由于无法找出这个字符集，这里显示的是正方形，实际应该是圆形。

f ∘ id = f  
id ∘ f = f

通过这个组合方式，我们看到单元函数其实也是一个单位元。

如果你想知道单位函数的名称从哪里来的，现在可以明白他是相对函数组合的单位元。