函数式编程

什么是Monoid？

　　首先我们需要了解什么是Monoid，才能了解什么是Monad。这一章是关于什么是Monoid。

　　一个monoid是一个元素(也可称对象)的集合，monoid首先是一个集合，但是这个集合有一些约束条件，也就是说，是一个特殊的集合，满足结合律和有元/幺元/么元，元/幺元/么元三个不同中文名称其实对应同一个英文Identity，这种元和其他元素结合时，并不会改变那些元素。

　　这里已经两次提到结合，其英文是associative，所谓结合律其实就是定义结合含义，通常百度定义为：

　　给定一个集合S上的二元运算·，如果对于S中的任意a,b,c。有：
　　a·(b·c) = (a·b)·c，
　　则称运算·满足结合律。

　　这是群论也就是范畴论的定义，群论或范畴论的英文是Category。群论可以看成是一种跨数学和计算机的高阶学科，那么在我们编程中这种结合律的定义是什么呢？

　　假设有一个函数输入类型是A，而输出类型是B：

B f(A a);

　　另外还有一个函数输入类型是B，输出类型是C:

C g(B b);

　　这两个函数分别是f和g。这两个函数组合在一起就会成为一个集合，组合代码如下：

C g_after_f(A a)

{

return g(f(a));

}

　　这个集合中有两个函数，还不能解释结合律是什么，现在我们再增加第三个函数h，这个函数是将C作为输入参数，输出类型是D:

D g(C c);

　　我们再将这三个函数组合在一起，组成一个集合，具体组合代码参考上面两个组合代码，非常类似，现在我们需要引入一个实心句号“.”来表达组合关系，f和g组合是g.f，g和h组合是h.g，其实这个实心句号就是前面组合代码的缩写，也要注意到前后顺序，g.f代表f和g的组合，也就是说，f函数的输出作为g函数的输入，而且f函数的输出类型必须和g函数的输入类型相同。

　　现在看看，三个函数组合，也就是f的输出作为g的输出类型，g的输出类型再作为h的输入类型，这样三个函数组合就是h.g.f，好了，结合律的意思就是：

h . (g . f) == (h . g) . f == h . g . f

　　我们解释第一公式h . (g . f)，其中括号的意思表示两个函数组合作为一个函数，也就是说f和g组合可看成一个函数(组合代码见前面)，组合的结果类型作为h的输入参数类型。这种公式的结果应该等同于(h . g) . f ，括号里是g和h的组合，这类似与f和g的组合代码，最后一个去掉括号，也就是说只要遵循首先计算f函数，其次是g，最后是h函数，至于在这种顺序下将任意两组作为一个单元都是一样的结果。这种结合符号类似加法。比如((5+3)+1 == 5+(3+1))；而减法则不是：((5-3)-1 != 5-(3-1))

　　前面我们说过，Monoid是一个满足结合律的特殊集合，现在我们知道我们三个函数的集合已经具备成为一个Monoid的条件，还有一个条件是满足有一个元素称为元/幺元/么元，这种元和其他元素结合时，并不会改变那些元素。所谓不改变那些元素，可以用公式表示如下：

e • a = a = a • e

　　其中e是一个元，e : 1 -> S公式表示S集合中的一个e元素，这个e元素与其他元素结合，不会改变那些元素。若e*a=a，e称为左单位元若a*e=a，e称为右单位元；若a*e=e*a=a，则e称为单位元。若该演算左右的元素能互换，左、右单位元相同，可称为双边单位元。

　　我们可以用具体数字案例说明这个公式，

0 + 7 == 7 + 0 == 7 这是e为0的加法
[] ++ [1,2,3] == [1,2,3] ++ [] == [1,2,3] 这可看成数组组合
{} union {apple} == {apple} union {} == {apple}

　　我们使用代码来说明这个元的定义，前面f函数的输入类型是A，输出类型是B，如果输出类型还是A自己，也就是如下：

A f(A a);

　　也就是说，一个函数的输入参数类型和返回类型是相同的，这个现象经常出现在我们编程实践中，而且是良好编程鼓励的风格。那么我们称为这个函数为元函数，identity function，C++的代码如下：

template<class T> T id(T x) { return x; }

　　那么一个输入输出都指向同一个类型的函数有什么用？这其实类似代数中0零一样，在组合中，零和任何数字组合(相加)都不会影响这些数字。

　　我们可以用简洁的语法表示这种指向自己类型的函数，也就是元/幺元法则：

id . f = f  -- 左单元
f . id = f  -- 右单元

　　结合律和幺元法则是Monoid的重要定义，也认为是范畴法则category law。在Haskell语言中，这种幺元法则可以简单表示如下：

id :: a -> a  
id x = x

范畴定义

　　现在我们对范畴Category进行一下总结性定义，范畴是由元素对象和态射箭头组成的，这个箭头开始端是一个元素对象，目的地也是一个元素对象。简单定义f:a → b或f::a → b，这两个是冒号区别，不同语言体系表达不同。

　　范畴虽然有两个部件：元素对象和态射箭头，这个态射箭头有两种，不同元素对象比如a和b之间的态射箭头称为组合箭头，而指向自己的箭头称为元箭头，或者单元，幺元。

　　总结范畴的元素对象和箭头态射的规则如下：

1.对于箭头 f:a → b 和箭头 g:b → c，如果有一个箭头 h: a → c ，那么就称为它们的组合，写法是：h = g ° f (或者h=g.f)
2. 对于每个元素对象，都有一个单元箭头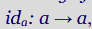：，对于任何
f: a → b下面肯定是真: 。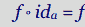
同样，对于任何g: c → a，我们也有：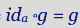
(这一段意思表达幺元(单元)与任何元素结合都不影响这些元素)
组合是符合结合律associative: f ° (g ° h) = (f ° g) ° h.

　　从上面看出，态射箭头有两种，一种是第一点的组合箭头，还有一种是第二点的单元箭头。

　　我们将一个范畴有元素对象和态射箭头，态射箭头有组合和幺元两种，且满足结合律，这种范畴称为Monoid。

　　在另外一些定义中，有广群这个概念：

　　对于某非空集合S ,若存在S上的二元运算"*"使得对于任意的a,b∈S,有a*b∈S（运算封闭），则称{S, *}为广群。

　　比较这个广群概念和前面范畴的定义，广群只是定义需要有一个集合，集合中有元素和操作，操作结果也属于这个集合，这样一个泛泛的集合称为广群。

　　如果广群再加上结合律约束，就会得到半群，因此半群是广群的子集，要求更苛刻些，而半群如果再加上幺元就是幺半群，也就是结合律+幺元=幺半群，所以，Monid对应的中文是幺半群。

　　总结：Monoid 是一个满足结合律的集合，每个Monoid元素都有一个identity幺元箭头，类似数据表的主键ID，实体标识一样，放在集合中，不会影响集合中其他元素，可以看成是一个人为的标识符号。

　　理解了Monoid，那么我们就能理解Monad，因为有一句经典大开脑洞的英文名言：

　　A monad is just a monoid in the category of endofunctors, what's the problem?

什么是Monad?